AI & Cloud by Syd

Part 4: attention is all you need (pretty much): From Basic Attention to Multi-Head Attention in PyTorch

In Part 3 of this series, I focused on preparing a dataset for training a language model, combining multiple books into a corpus, tokenizing with tiktoken, and creating PyTorch datasets. With the data pipeline in place, the next step in building a GPT-style model is to understand attention mechanisms.

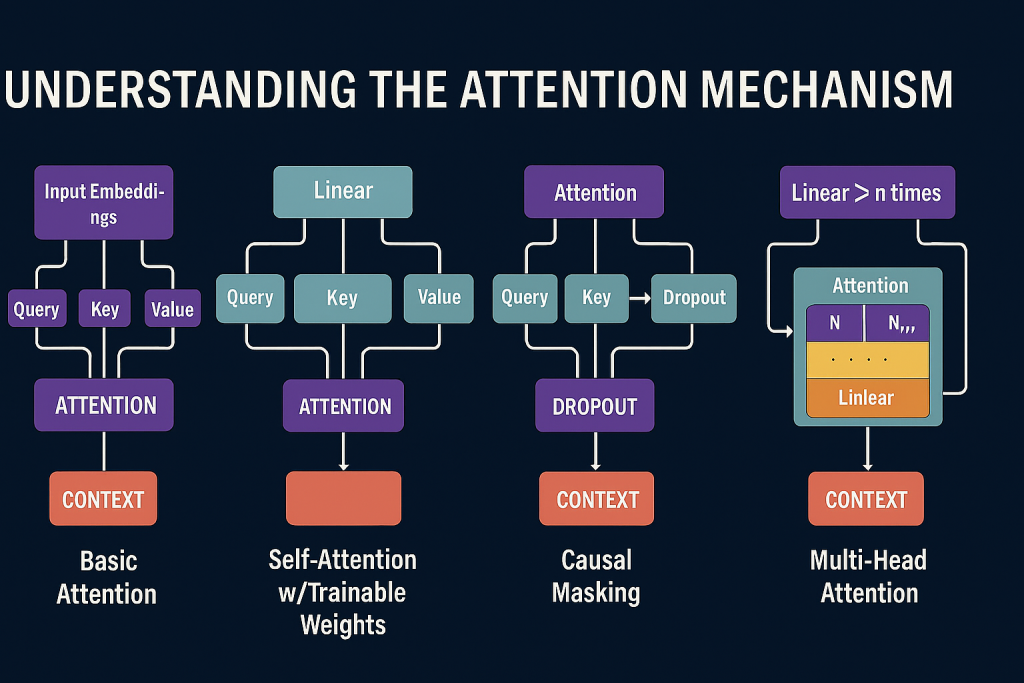
Attention is the core innovation behind transformers. It allows models to dynamically focus on different parts of an input sequence, capturing dependencies across long contexts without recurrence. In this post, I will walk through my journey of implementing attention in PyTorch, starting from the most basic dot-product attention without trainable weights, and building up to a reusable multi-head attention module.

Why Attention?

Traditional sequence models like RNNs and LSTMs process tokens step by step, which makes it difficult to capture long-range dependencies. Attention solves this by allowing every token to directly interact with every other token in the sequence. The mechanism is built around three concepts:

  • Query (Q): What we are looking for.
  • Key (K): What each token offers.
  • Value (V): The information carried by each token.

By comparing queries with keys, we compute attention scores that determine how much weight to give each value when forming a context vector.

Step 1: Basic Attention Without Trainable Weights

I began with a simple example: computing attention scores using dot products between a query and embeddings. This helped me understand the mechanics before adding trainable parameters.

example_input_embeddings = torch.tensor([
    [0.23, 0.87, 0.45],
    [0.12, 0.76, 0.34],
    [0.98, 0.54, 0.21],
    [0.67, 0.39, 0.88],
    [0.53, 0.29, 0.74],
    [0.41, 0.65, 0.32]
])

print(example_input_embeddings.shape)

example_query = example_input_embeddings[1]
example_attention_scores = torch.empty(example_input_embeddings.shape[0])
for i, embedding in enumerate(example_input_embeddings):
    example_attention_scores[i] = torch.dot(example_query, embedding)

print(f"Example attention scores for 2nd query: {example_attention_scores}")

This produces raw attention scores, which are then normalized with softmax to form probability-like weights.

normalized_example_attention_scores = torch.softmax(example_attention_scores, dim = 0)
print(f"Normalized attention scores for 2nd query: {normalized_example_attention_scores}")

Finally, the context vector is computed as a weighted sum of embeddings:

example_context_vector = torch.zeros(example_query.shape)
for i, embedding in enumerate(example_input_embeddings):
    example_context_vector += normalized_example_attention_scores[i] * embedding
print(f"Context vector for 2nd query: {example_context_vector}")

This completes the simplest form of attention.

Step 2: Scaling Up with Matrix Multiplication

Instead of computing scores with loops, we can use matrix multiplication to calculate all pairwise attention scores efficiently:

all_attention_scores = example_input_embeddings @ example_input_embeddings.T
print(f"All attention scores using matrix multiplication:\n {all_attention_scores}")

Applying softmax row-wise normalizes the scores for each query:

all_normalized_attention_scores = torch.softmax(all_attention_scores, dim = -1)
print(f"All normalized attention scores:\n {all_normalized_attention_scores}")

And context vectors for all queries can be computed in parallel:

all_example_context_vectors = all_normalized_attention_scores @ example_input_embeddings
print(f"All context vectors using matrix multiplication:\n {all_example_context_vectors}")

This is the foundation of self-attention.

Step 3: Introducing Trainable Projections

In transformers, queries, keys, and values are not just the raw embeddings. They are learned projections. Using linear transformations, each input embedding is mapped into Q, K, and V spaces.

example_input = example_input_embeddings[1]
input_dim = example_input_embeddings.shape[1]
output_dim = 2

torch.manual_seed(246)
weight_query = torch.nn.Parameter(torch.rand(input_dim, output_dim), requires_grad = True)
weight_key = torch.nn.Parameter(torch.rand(input_dim, output_dim), requires_grad = True)
weight_value = torch.nn.Parameter(torch.rand(input_dim, output_dim), requires_grad = True)

example_query = example_input @ weight_query
example_key = example_input @ weight_key
example_value = example_input @ weight_value

This step introduces trainable parameters, allowing the model to learn how best to represent tokens for attention.

Step 4: Building a Self-Attention Module

To make attention reusable, I wrapped it in a PyTorch module. This encapsulates the entire process: projecting Q, K, V, computing scores, applying scaling and softmax, and generating context vectors.

import torch.nn as nn
class SelfAttention(nn.Module):
    def __init__(self, input_dim, output_dim):
        super().__init__()
        self.weight_query = nn.Parameter(torch.rand(input_dim, output_dim))
        self.weight_key = nn.Parameter(torch.rand(input_dim, output_dim))
        self.weight_value = nn.Parameter(torch.rand(input_dim, output_dim))
    
    def forward(self, x):
        queries = x @ self.weight_query
        keys = x @ self.weight_key
        values = x @ self.weight_value
        attention_scores = queries @ keys.T
        scaling_factor = keys.shape[-1] ** 0.5
        attention_weights = torch.softmax(attention_scores / scaling_factor, dim = -1)
        context_vector = attention_weights @ values
        return context_vector

Using this module:

torch.manual_seed(246)
self_attention = SelfAttention(input_dim, output_dim)
context_vectors = self_attention(example_input_embeddings)
print(f"Context vectors from SelfAttention module:\n {context_vectors}")

Step 5: Enhancements: Linear Layers, Causal Masking, Dropout

I then extended the module to use nn.Linear layers with optional bias (SelfAttentionv2), added causal masking to prevent tokens from attending to the future, and applied dropout for regularization. These are critical for autoregressive models like GPT.

Causal masking ensures that predictions at position t only depend on tokens up to t. Dropout helps prevent overfitting by randomly zeroing out attention weights during training.

Step 6: Multi-Head Attention

Finally, I implemented multi-head attention, where multiple attention heads run in parallel, each learning different relationships. Their outputs are concatenated and projected back to the model dimension.

class MultiHeadAttention(nn.Module):
    def __init__(self, input_dim, output_dim, dropout, context_length, num_heads, qkv_bias = False):
        super().__init__()
        assert output_dim % num_heads == 0, "Output dimension must be divisible by number of heads"
        self.output_dim = output_dim
        self.num_heads = num_heads
        self.head_dim = output_dim // num_heads
        self.weight_query = nn.Linear(input_dim, output_dim, qkv_bias)
        self.weight_key = nn.Linear(input_dim, output_dim, qkv_bias)
        self.weight_value = nn.Linear(input_dim, output_dim, qkv_bias)
        self.dropout = nn.Dropout(dropout)
        self.register_buffer("causal_mask", torch.triu(torch.ones(context_length, context_length), diagonal = 1))
        self.output_projection = nn.Linear(output_dim, output_dim)
    
    def forward(self, x):
        batch_size, num_tokens, _ = x.shape
        queries = self.weight_query(x).view(batch_size, num_tokens, self.num_heads, self.head_dim).transpose(1,2)
        keys = self.weight_key(x).view(batch_size, num_tokens, self.num_heads, self.head_dim).transpose(1,2)
        values = self.weight_value(x).view(batch_size, num_tokens, self.num_heads, self.head_dim).transpose(1,2)
        attention_scores = queries @ keys.transpose(2,3)
        attention_scores.masked_fill_(self.causal_mask.bool()[:num_tokens, :num_tokens], -torch.inf)
        attention_weights = torch.softmax(attention_scores / keys.shape[-1]**0.5, dim = -1)
        attention_weights = self.dropout(attention_weights)
        context_vectors = self.output_projection((attention_weights @ values).transpose(1,2).contiguous().view(batch_size, num_tokens, self.output_dim))
        return context_vectors

This is the same mechanism used in GPT and other transformer models.

Lessons Learned

  • Starting with simple dot products clarified the mechanics of attention.
  • Softmax normalization is essential for interpretability and stability.
  • Linear projections allow the model to learn flexible Q, K, V representations.
  • Causal masking is critical for autoregressive tasks like language modeling.
  • Multi‑head attention provides richer sequence representations by letting the model attend to different aspects of the input in parallel.
  • Wrapping attention into modular PyTorch classes makes it reusable and easy to extend into full transformer blocks.

Try It Yourself

The full notebook with all the steps, from basic attention to multi‑head attention, is available here:

👉 Attention Mechanisms Repository

Clone the repo, open the Jupyter notebook, and step through the code. You can experiment with different numbers of heads, embedding dimensions, and masking strategies to see how they affect the outputs.

Build It Yourself

If you want to try building it yourself, you can find the complete code with detailed explanations of each block in the source code section at the end of this post. All the best!

What’s Next

With attention mechanisms implemented, the next step is to assemble the transformer block itself. In Part 5, I’ll combine multi‑head attention with feed‑forward layers, residual connections, and normalization to build the backbone of a GPT‑style model. From there, we’ll be ready to start stacking blocks and training a small‑scale transformer.

Source Code

attention

admin

, ,

Leave a Reply

Your email address will not be published. Required fields are marked *