In Part 4, I focused on attention and built reusable modules that mirror transformer internals. In Part 5, I assembled the complete GPT architecture at medium scale, validated shapes and memory, and ran first text generation. The outputs are gibberish because the model is untrained. That is expected.
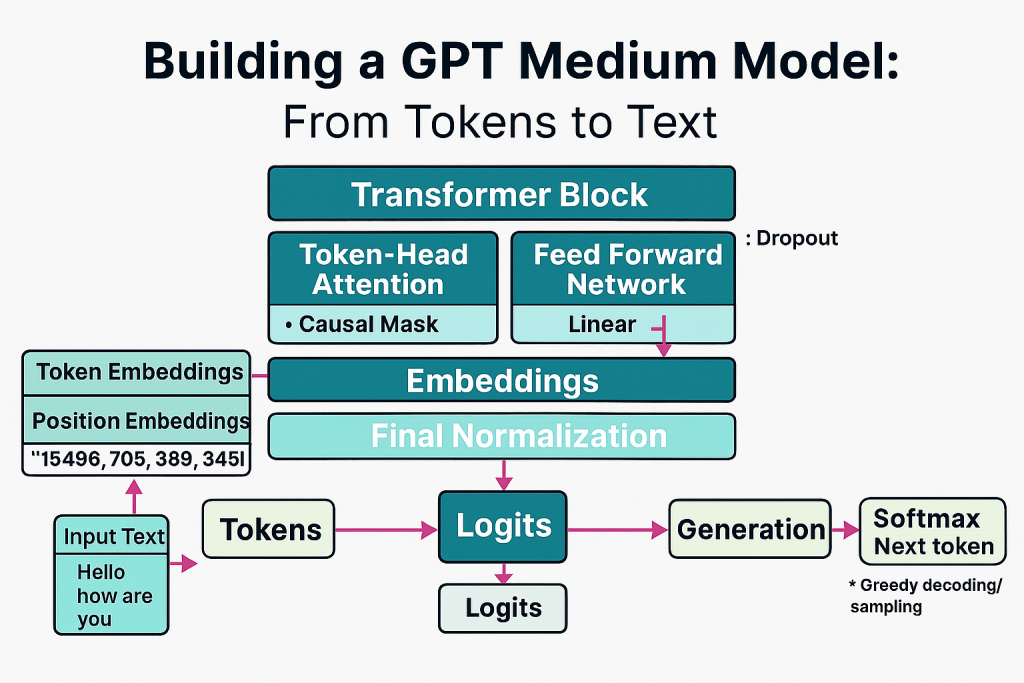
The goal here is to make sure the architecture is sound and the end-to-end pipeline works. In Part 6, I will pre-train the model.
Model configuration and setup
This configuration targets a GPT-2 medium scale model, closely mirroring common hyperparameters at that size.
SYDSGPT_CONFIG_345M = {
"vocab_size" : 50257,
"context_length" : 1024,
"embedding_dim" : 1024,
"num_heads" : 16,
"num_layers" : 24,
"dropout" : 0.1,
"qkv_bias" : False
}- Context length: 1,024
- Embedding dim: 1,024
- Heads: 16
- Layers: 24
- Dropout: 0.1
- QKV bias: False
Placeholder GPT for structure validation
I begin with a skeleton GPT to validate the computation graph and shapes. This wires embeddings, a stack of transformer blocks, layer norm, and output projection.
class PlaceholderGPT(nn.Module):
def __init__(self, config):
super().__init__()
self.token_embedding = nn.Embedding(config["vocab_size"], config["embedding_dim"])
self.position_embedding = nn.Embedding(config["context_length"], config["embedding_dim"])
self.dropout = nn.Dropout(config["dropout"])
self.transformer_blocks = nn.Sequential(*[PlaceholderTransformerBlock(config) for _ in range(config["num_layers"])])
self.final_layer_norm = PlaceholderLayerNorm(config["embedding_dim"])
self.output_projection = nn.Linear(config["embedding_dim"], config["vocab_size"], bias = False)
def forward(self, input):
batch_size, seq_length = input.shape
token_embeddings = self.token_embedding(input)
position_embeddings = self.position_embedding(torch.arange(seq_length, device = input.device))
x = token_embeddings + position_embeddings
x = self.dropout(x)
x = self.transformer_blocks(x)
x = self.final_layer_norm(x)
logits = self.output_projection(x)
return logits
class PlaceholderTransformerBlock(nn.Module):
def __init__(self, config):
super().__init__()
def forward(self, x):
return x
class PlaceholderLayerNorm(nn.Module):
def __init__(self, embedding_dim, eps = 1e-5):
super().__init__()
def forward(self, x):
return xTokenization and forward pass sanity check
I validate that the forward pass produces logits of shape (batch, seq_len, vocab_size) using GPT-2 tokenizer.
tokenizer = tiktoken.get_encoding("gpt2")
batch = []
ex1 = "Hello how are you"
ex2 = "What are you doing"
batch.append(torch.tensor(tokenizer.encode(ex1)))
batch.append(torch.tensor(tokenizer.encode(ex2)))
batch = torch.stack(batch, dim = 0)
print(batch)
torch.manual_seed(246)
test_model = PlaceholderGPT(SYDSGPT_CONFIG_345M)
logits = test_model(batch)
print(f"Logits Shape: {logits.shape}")
print(f"Logits: \n {logits}")Expected shape:
Logits Shape: torch.Size([2, 4, 50257])This confirms correct wiring from embeddings to output projection.
Manual layer normalization demonstration
Before using a custom class, I show manual normalization to verify behavior.
torch.manual_seed(246)
ex_batch = torch.randn(2,6)
nn_layer = nn.Sequential(nn.Linear(6,8), nn.ReLU())
output = nn_layer(ex_batch)
print(f"Output Shape: {output.shape}")
print(f"Output: \n {output}")
mean = output.mean(dim = -1, keepdim = True)
variance = output.var(dim = -1, keepdim = True)
print(f"Mean: \n {mean}")
print(f"Variance: \n {variance}")
normalized_output = (output - mean) / torch.sqrt(variance)
mean_after_norm = normalized_output.mean(dim = -1, keepdim = True)
variance_after_norm = normalized_output.var(dim = -1, keepdim = True)
print(f"Normalized Output: \n {normalized_output}")
print(f"Mean After Norm: \n {mean_after_norm}")
print(f"Variance After Norm: \n {variance_after_norm}")- Observation: Per-sample mean close to zero and variance near one.
Custom LayerNorm implementation and usage
This LayerNorm mirrors the behavior of PyTorch’s builtin but is implemented from scratch for clarity.
class LayerNorm(nn.Module):
def __init__(self, embedding_dim, eps = 1e-5):
super().__init__()
self.eps = eps
self.scale = nn.Parameter(torch.ones(embedding_dim))
self.shift = nn.Parameter(torch.zeros(embedding_dim))
def forward(self, x):
mean = x.mean(dim = -1, keepdim = True)
variance = x.var(dim = -1, keepdim = True, unbiased = False)
normalized_x = (x - mean) / torch.sqrt(variance + self.eps)
return self.scale * normalized_x + self.shiftUsage example:
layer_norm = LayerNorm(embedding_dim = 6)
normalized_output = layer_norm(ex_batch)
print(f"Layer Norm Output: \n {normalized_output}")
mean_after_norm = normalized_output.mean(dim = -1, keepdim = True)
variance_after_norm = normalized_output.var(dim = -1, keepdim = True, unbiased = False)
print(f"Mean After Layer Norm: \n {mean_after_norm}")
print(f"Variance After Layer Norm: \n {variance_after_norm}")- Observation: LayerNorm maintains mean near zero and variance near one with learnable scale and shift.
GELU activation from first principles
GELU is the default activation in transformer FFNs.
class GELU(nn.Module):
def __init__(self):
super().__init__()
def forward(self, x):
return 0.5 * x *(1 + torch.tanh(torch.sqrt(torch.tensor(2.0 / torch.pi)) * (x + 0.044715 * torch.pow(x, 3))))FeedForward network construction and run
Transformer FFN expands and contracts the embedding dimension with GELU nonlinearity.
class FeedForward(nn.Module):
def __init__(self, config):
super().__init__()
self.layers = nn.Sequential(
nn.Linear(config["embedding_dim"], 4 * config["embedding_dim"]),
GELU(),
nn.Linear(4 * config["embedding_dim"], config["embedding_dim"])
)
def forward(self, x):
return self.layers(x)Example usage:
feed_forward = FeedForward(SYDSGPT_CONFIG_345M)
example_input = torch.randn(2, 6, SYDSGPT_CONFIG_345M["embedding_dim"])
output = feed_forward(example_input)
print(f"Feed Forward Output Shape: {output.shape}")
print(f"Feed Forward Output: \n {output}")Observation: Output shape preserves (batch, seq_len, embedding_dim).
Residual connections and gradient flow
Residuals are essential for training deep networks. This experiment shows gradients are healthier with residuals.
class ResidualConnectionsTestNN(nn.Module):
def __init__(self, layer_dims, use_shortcuts):
super().__init__()
self.use_shortcuts = use_shortcuts
self.layers = nn.ModuleList([
nn.Sequential(nn.Linear(layer_dims[0], layer_dims[1]), GELU()),
nn.Sequential(nn.Linear(layer_dims[1], layer_dims[2]), GELU()),
nn.Sequential(nn.Linear(layer_dims[2], layer_dims[3]), GELU()),
nn.Sequential(nn.Linear(layer_dims[3], layer_dims[4]), GELU()),
nn.Sequential(nn.Linear(layer_dims[4], layer_dims[5]), GELU()),
nn.Sequential(nn.Linear(layer_dims[5], layer_dims[6]), GELU())
])
def forward(self, x):
for layer in self.layers:
layer_output = layer(x)
if self.use_shortcuts and x.shape == layer_output.shape:
x = x + layer_output
else:
x = layer_output
return x
def get_gradients(model, input):
output = model(input)
target = torch.tensor([[0.]])
loss_function = nn.MSELoss()
loss = loss_function(output, target)
loss.backward()
for name, param in model.named_parameters():
if 'weight' in name:
print(f"Mean of Gradients for {name}: {param.grad.abs().mean().item()}")
layer_dims = [3, 3, 3, 3, 3, 3, 1]
input = torch.tensor([[-1., 0., 1.]])
torch.manual_seed(246)
model_without_residuals = ResidualConnectionsTestNN(layer_dims, use_shortcuts = False)
torch.manual_seed(246)
model_with_residuals = ResidualConnectionsTestNN(layer_dims, use_shortcuts = True)
print("Gradients without Residual Connections:")
get_gradients(model_without_residuals, input)
print("Gradients with Residual Connections:")
get_gradients(model_with_residuals, input)Observation: Residual connections increase and stabilize gradients across layers.
Transformer block with attention, FFN, layer norm, dropout, and residuals
A single transformer block combines everything into the standard pre-norm residual structure.
from attention.MultiHeadAttention import MultiHeadAttention
class TransformerBlock(nn.Module):
def __init__(self, config):
super().__init__()
self.attention = MultiHeadAttention(
input_dim = config["embedding_dim"],
output_dim = config["embedding_dim"],
dropout = config["dropout"],
context_length = config["context_length"],
num_heads = config["num_heads"],
qkv_bias = config["qkv_bias"])
self.layer_norm1 = LayerNorm(config["embedding_dim"])
self.feed_forward = FeedForward(config)
self.layer_norm2 = LayerNorm(config["embedding_dim"])
self.dropout = nn.Dropout(config["dropout"])
def forward(self, x):
shortcut = x
x = self.layer_norm1(x)
x = self.attention(x)
x = self.dropout(x)
x = x + shortcut
shortcut = x
x = self.layer_norm2(x)
x = self.feed_forward(x)
x = self.dropout(x)
x = x + shortcut
return xRunning the block:
torch.manual_seed(246)
transformer = TransformerBlock(SYDSGPT_CONFIG_345M)
example_input = torch.randn(2, 6, SYDSGPT_CONFIG_345M["embedding_dim"])
output = transformer(example_input)
print(f"Example Input Shape: {example_input.shape}")
print(f"Transformer Block Output Shape: {output.shape}")
print(f"Transformer Block Output: \n {output}")Observation: The block preserves shape (batch, seq_len, embedding_dim).
Full SydsGPT model assembly
The complete GPT model stacks multiple transformer blocks and adds embeddings and final projection
class SydsGPT(nn.Module):
def __init__(self, config):
super().__init__()
self.token_embedding = nn.Embedding(config["vocab_size"], config["embedding_dim"])
self.position_embedding = nn.Embedding(config["context_length"], config["embedding_dim"])
self.drop_embedding = nn.Dropout(config["dropout"])
self.transformer_blocks = nn.Sequential(*[TransformerBlock(config) for _ in range(config["num_layers"])])
self.final_layer_norm = LayerNorm(config["embedding_dim"])
self.output_projection = nn.Linear(config["embedding_dim"], config["vocab_size"], bias = False)
def forward(self, input):
batch_size, seq_length = input.shape
token_embeddings = self.token_embedding(input)
position_embeddings = self.position_embedding(torch.arange(seq_length, device=input.device))
x = token_embeddings + position_embeddings
x = self.drop_embedding(x)
x = self.transformer_blocks(x)
x = self.final_layer_norm(x)
logits = self.output_projection(x)
return logitsForward pass on tokenized inputs
torch.manual_seed(246)
sydsgpt_model = SydsGPT(SYDSGPT_CONFIG_345M)
logits = sydsgpt_model(batch)
print(f"Input: {batch}")
print(f"Logits Shape: {logits.shape}")
print(f"Logits: {logits}")Observation: Logits shape (batch, seq_len, vocab) matches expectations.
Parameter count and memory footprint
I compute the total trainable parameters and estimate memory usage at float32
total_parameters = sum(parameter.numel() for parameter in sydsgpt_model.parameters())
print(f"Total Parameters in SydsGPT Model: {total_parameters}")
total_size_bytes = total_parameters * 4
total_size_mb = total_size_bytes / (1024 ** 2)
print(f"Total Model Size: {total_size_mb:.2f} MB")- Result: 406,212,608 parameters
- Size: ~1,549.58 MB in float32 for parameters alone
This excludes activations, gradients, optimizer states
Greedy text generation loop
A simple autoregressive loop that uses argmax decoding. It respects the context window and extends sequences token by token.
def generate_simple(model, input_ids, max_length, context_size):
for _ in range(max_length):
input_ids_crop = input_ids[:, -context_size:]
with torch.no_grad():
logits = model(input_ids_crop)
next_token_logits = logits[:, -1, :]
next_token_probs = torch.softmax(next_token_logits, dim = -1)
next_token = torch.argmax(next_token_probs, dim = -1, keepdim = True)
input_ids = torch.cat((input_ids, next_token), dim = 1)
return input_idsUse it end to end:
start_context = "Once upon a time"
encoded_context = tokenizer.encode(start_context)
input_ids = torch.tensor(encoded_context).unsqueeze(0)
print(f"Encoded Context: {encoded_context}")
print(f"Input IDs Shape: {input_ids.shape}")
sydsgpt_model.eval()
context_size = SYDSGPT_CONFIG_345M["context_length"]
generated_ids = generate_simple(sydsgpt_model, input_ids, 10, context_size)
print(f"Generated IDs: {generated_ids}")
generated_text = tokenizer.decode(generated_ids.squeeze(0).tolist())
print(f"Generated Text: {generated_text}")Observation: The output text is gibberish. This is expected since the model is untrained. The goal is verifying the generation loop and context handling.
What I validated in Part 5
- Architecture completeness: Embeddings, transformer blocks, normalization, residuals, and projection are wired correctly.
- Shape discipline: Every component preserves the expected shapes through the stack.
- Parameter scale and memory: The model lands at ~406M parameters with an appropriate memory footprint for float32 weights.
- Generation pipeline: Tokenization, forward pass, logits to next token, and sequence extension work as expected.
- Stability building blocks: LayerNorm, GELU, FFN, and residual connections are correctly implemented and behaving as intended.
Try It Yourself
The full notebook with all the steps, from basic attention to multi‑head attention, is available here:
SydsGPT notebook Repository
Clone the repo, open the Jupyter notebook, and step through the code. You can experiment with different numbers of heads, embedding dimensions, and masking strategies to see how they affect the outputs.
Build It Yourself
If you want to try building it yourself, you can find the complete code with detailed explanations of each block in the source code section at the end of this post. All the best!
What’s next
Part 6 is pre-training. I will set up the training loop with tokenized corpora, define the loss function for next-token prediction, implement batching at scale, and start training with a robust optimizer. I may also switch to mixed precision to reduce memory and speed up training. The goal is to move from gibberish to coherent text by optimizing on a meaningful dataset.
Source Code
import torch
import torch.nn as nn
import tiktoken
SYD’S GPT-345M Model Configuration¶
This notebook cell defines the configuration dictionary for a GPT-style language model with approximately 345 million parameters. The configuration parameters are as follows:
- vocab_size: The number of unique tokens (words, subwords, or characters) that the model can understand. For GPT-345M, this is set to 50,257, matching the standard GPT-2 vocabulary size.
- context_length: The maximum number of tokens the model can consider in a single input sequence. Here, it is set to 1,024 tokens, which determines the model’s memory window for generating or analyzing text.
- embedding_dim: The size of the vector used to represent each token. A higher embedding dimension allows the model to capture more nuanced relationships between tokens. This configuration uses 1,024 dimensions.
- num_heads: The number of attention heads in the multi-head self-attention mechanism. More heads allow the model to focus on different parts of the input simultaneously. This model uses 16 heads.
- num_layers: The number of transformer blocks (layers) stacked in the model. More layers generally increase the model’s capacity to learn complex patterns. Here, 24 layers are used.
- dropout: The dropout rate applied during training to prevent overfitting. A value of 0.1 means 10% of the connections are randomly dropped during each training step.
- qkv_bias: A boolean indicating whether to include a bias term in the query, key, and value projections of the attention mechanism. Setting this to
Falsemeans no bias is added.
This configuration is typical for a medium-sized GPT-2 model and can be used as a starting point for training or fine-tuning a transformer-based language model.
SYDSGPT_CONFIG_345M = {
"vocab_size" : 50257,
"context_length" : 1024,
"embedding_dim" : 1024,
"num_heads" : 16,
"num_layers" : 24,
"dropout" : 0.1,
"qkv_bias" : False
}
PlaceholderGPT Model Class Overview¶
The following code cell defines a simplified, illustrative version of a GPT-style transformer model using PyTorch. This implementation is intended for educational purposes and demonstrates the core architectural components of a transformer-based language model:
Main Components¶
PlaceholderGPT (nn.Module): The main model class. It initializes the following layers:
- Token Embedding: Maps each token in the input sequence to a high-dimensional vector.
- Position Embedding: Adds positional information to each token, allowing the model to distinguish between tokens at different positions.
- Dropout Layer: Regularizes the model by randomly dropping units during training to prevent overfitting.
- Transformer Blocks: A stack of placeholder transformer blocks (not fully implemented here) that would normally perform self-attention and feed-forward operations.
- Final Layer Normalization: Normalizes the output of the transformer blocks.
- Output Projection: Projects the final hidden states to the vocabulary size, producing logits for each token.
forward(input): The forward pass of the model. It processes the input sequence through embeddings, dropout, transformer blocks, layer normalization, and output projection to produce logits for each token position.
Supporting Classes¶
PlaceholderTransformerBlock (nn.Module): Represents a single transformer block. In a full implementation, this would include multi-head self-attention and feed-forward layers. Here, it simply returns the input unchanged.
PlaceholderLayerNorm (nn.Module): A placeholder for layer normalization. In a real model, this would normalize the input tensor across the embedding dimension.
What does eps = 1e-5 mean?¶
In the context of neural networks and layer normalization, eps (epsilon) is a small constant added to the denominator when normalizing activations. This prevents division by zero and improves numerical stability.
- Value:
1e-5means epsilon is set to $0.00001$. - Purpose: When calculating the normalized output, the formula typically looks like: $$ \text{normalized} = \frac{x – \mu}{\sqrt{\sigma^2 + \epsilon}} $$ where $\mu$ is the mean and $\sigma^2$ is the variance of the input $x$.
- Why needed: If the variance is very close to zero, adding epsilon ensures the denominator is never zero, avoiding undefined results and improving stability during training.
This is a standard practice in deep learning layers such as batch normalization and layer normalization.
Notes¶
- This code is a skeleton and does not implement the full transformer logic (e.g., attention mechanisms, feed-forward networks, or actual layer normalization).
- The model uses configuration parameters such as
vocab_size,embedding_dim,context_length,num_layers, anddropoutfrom the configuration dictionary defined earlier in the notebook. - The purpose of this cell is to illustrate the structure and flow of a transformer-based language model in PyTorch, serving as a starting point for further development or experimentation.
class PlaceholderGPT(nn.Module):
def __init__(self, config):
super().__init__()
self.token_embedding = nn.Embedding(config["vocab_size"], config["embedding_dim"])
self.position_embedding = nn.Embedding(config["context_length"], config["embedding_dim"])
self.dropout = nn.Dropout(config["dropout"])
self.transformer_blocks = nn.Sequential(*[PlaceholderTransformerBlock(config) for _ in range(config["num_layers"])])
self.final_layer_norm = PlaceholderLayerNorm(config["embedding_dim"])
self.output_projection = nn.Linear(config["embedding_dim"], config["vocab_size"], bias = False)
def forward(self, input):
batch_size, seq_length = input.shape
token_embeddings = self.token_embedding(input)
position_embeddings = self.position_embedding(torch.arange(seq_length, device = input.device))
x = token_embeddings + position_embeddings
x = self.dropout(x)
x = self.transformer_blocks(x)
x = self.final_layer_norm(x)
logits = self.output_projection(x)
return logits
class PlaceholderTransformerBlock(nn.Module):
def __init__(self, config):
super().__init__()
def forward(self, x):
return x
class PlaceholderLayerNorm(nn.Module):
def __init__(self, embedding_dim, eps = 1e-5):
super().__init__()
def forward(self, x):
return x
Example: Tokenization and Model Forward Pass¶
This code cell demonstrates how to tokenize input text, prepare a batch for the model, and run a forward pass using the PlaceholderGPT model defined earlier in the notebook.
Steps Explained¶
Tokenization
- Uses the
tiktokenlibrary to obtain the GPT-2 tokenizer. - Two example sentences (
ex1andex2) are encoded into lists of token IDs.
- Uses the
Batch Preparation
- The encoded token lists are converted to PyTorch tensors and added to a batch list.
- The batch is stacked into a single tensor with shape
(batch_size, sequence_length). - The batch tensor is printed to show its contents.
Model Initialization and Forward Pass
- Sets a manual random seed for reproducibility.
- Instantiates the
PlaceholderGPTmodel with the configuration dictionary. - Runs the batch through the model to obtain logits (unnormalized predictions for each token position).
Output
- Prints the shape of the logits tensor, which should be
(batch_size, sequence_length, vocab_size). - Prints the actual logits tensor values.
- Prints the shape of the logits tensor, which should be
Notes¶
- This example uses a placeholder model, so the logits are not meaningful predictions but demonstrate the expected output structure.
- The code illustrates the typical workflow for preparing text data and running it through a transformer-based language model in PyTorch.
- The use of
torch.manual_seedensures that results are reproducible for debugging and experimentation.
tokenizer = tiktoken.get_encoding("gpt2")
batch = []
ex1 = "Hello how are you"
ex2 = "What are you doing"
batch.append(torch.tensor(tokenizer.encode(ex1)))
batch.append(torch.tensor(tokenizer.encode(ex2)))
batch = torch.stack(batch, dim = 0)
print(batch)
torch.manual_seed(246)
test_model = PlaceholderGPT(SYDSGPT_CONFIG_345M)
logits = test_model(batch)
print(f"Logits Shape: {logits.shape}")
print(f"Logits: \n {logits}")
tensor([[15496, 703, 389, 345],
[ 2061, 389, 345, 1804]])
Logits Shape: torch.Size([2, 4, 50257])
Logits:
tensor([[[ 0.2638, -0.1249, -1.9838, ..., -0.0289, 0.6842, -0.1247],
[-0.0896, 1.0701, 0.0236, ..., 0.4069, -0.5886, -0.4666],
[ 0.6501, 0.0914, -1.0634, ..., 1.0771, 0.1660, -0.0224],
[ 0.5803, 0.3458, -0.4553, ..., 0.7233, -1.3835, -0.2096]],
[[ 1.6676, 0.5273, -0.3480, ..., -0.0478, -0.2177, 0.0361],
[ 0.6377, -0.6156, -1.3517, ..., 1.0306, -1.0850, -1.3458],
[ 0.1607, 0.2084, 0.6130, ..., 0.6961, -0.9398, 0.6000],
[-0.1086, -0.2255, -0.4622, ..., 0.8606, 0.1524, -1.0448]]],
grad_fn=<UnsafeViewBackward0>)
Logits Shape: torch.Size([2, 4, 50257])
Logits:
tensor([[[ 0.2638, -0.1249, -1.9838, ..., -0.0289, 0.6842, -0.1247],
[-0.0896, 1.0701, 0.0236, ..., 0.4069, -0.5886, -0.4666],
[ 0.6501, 0.0914, -1.0634, ..., 1.0771, 0.1660, -0.0224],
[ 0.5803, 0.3458, -0.4553, ..., 0.7233, -1.3835, -0.2096]],
[[ 1.6676, 0.5273, -0.3480, ..., -0.0478, -0.2177, 0.0361],
[ 0.6377, -0.6156, -1.3517, ..., 1.0306, -1.0850, -1.3458],
[ 0.1607, 0.2084, 0.6130, ..., 0.6961, -0.9398, 0.6000],
[-0.1086, -0.2255, -0.4622, ..., 0.8606, 0.1524, -1.0448]]],
grad_fn=<UnsafeViewBackward0>)
Example: Manual Layer Normalization in PyTorch¶
This code cell demonstrates how to manually normalize the output of a neural network layer in PyTorch, illustrating the concept behind layer normalization.
Steps Explained¶
Batch and Layer Setup
- Sets a manual random seed for reproducibility.
- Creates a random batch tensor
ex_batchof shape(2, 6). - Defines a simple neural network layer (
nn_layer) consisting of a linear transformation followed by a ReLU activation. - Passes the batch through the layer to obtain
output. - Prints the shape and values of the output tensor.
Mean and Variance Calculation
- Computes the mean and variance of the output tensor along the last dimension (features) for each sample in the batch.
- Prints the mean and variance values.
Manual Normalization
- Normalizes the output tensor by subtracting the mean and dividing by the square root of the variance (without epsilon for simplicity).
- Prints the normalized output tensor.
- Calculates and prints the mean and variance of the normalized output to verify that the mean is close to zero and the variance is close to one for each sample.
Notes¶
- This example shows the core idea behind layer normalization, which is commonly used in deep learning models to stabilize and accelerate training.
- In practice, a small epsilon value is added to the denominator to prevent division by zero and improve numerical stability.
- The normalization is performed per sample (row) in the batch, across the feature dimension.
- This manual approach helps illustrate what built-in PyTorch layers like
nn.LayerNormdo internally.
torch.manual_seed(246)
ex_batch = torch.randn(2,6)
nn_layer = nn.Sequential(nn.Linear(6,8), nn.ReLU())
output = nn_layer(ex_batch)
print(f"Output Shape: {output.shape}")
print(f"Output: \n {output}")
mean = output.mean(dim = -1, keepdim = True)
variance = output.var(dim = -1, keepdim = True)
print(f"Mean: \n {mean}")
print(f"Variance: \n {variance}")
normalized_output = (output - mean) / torch.sqrt(variance)
mean_after_norm = normalized_output.mean(dim = -1, keepdim = True)
variance_after_norm = normalized_output.var(dim = -1, keepdim = True)
print(f"Normalized Output: \n {normalized_output}")
print(f"Mean After Norm: \n {mean_after_norm}")
print(f"Variance After Norm: \n {variance_after_norm}")
Output Shape: torch.Size([2, 8])
Output:
tensor([[0.0000, 1.4358, 0.8909, 0.0000, 0.3553, 1.4952, 0.0000, 0.0000],
[1.4236, 0.0000, 0.0000, 2.0742, 1.7022, 0.1547, 0.0589, 0.0000]],
grad_fn=<ReluBackward0>)
Mean:
tensor([[0.5221],
[0.6767]], grad_fn=<MeanBackward1>)
Variance:
tensor([[0.4337],
[0.7986]], grad_fn=<VarBackward0>)
Normalized Output:
tensor([[-0.7929, 1.3874, 0.5599, -0.7929, -0.2533, 1.4775, -0.7929, -0.7929],
[ 0.8357, -0.7572, -0.7572, 1.5638, 1.1475, -0.5841, -0.6913, -0.7572]],
grad_fn=<DivBackward0>)
Mean After Norm:
tensor([[0.0000e+00],
[2.2352e-08]], grad_fn=<MeanBackward1>)
Variance After Norm:
tensor([[1.],
[1.]], grad_fn=<VarBackward0>)
Improved Custom LayerNorm Class in PyTorch¶
This code cell presents an improved custom implementation of the Layer Normalization operation, a key technique for stabilizing and accelerating training in deep learning models, especially transformers.
How This Implementation Works¶
Class Definition:
LayerNorminherits fromnn.Modulefor seamless integration with PyTorch models.- The constructor accepts
embedding_dim(the size of the last dimension to normalize) andeps(a small constant for numerical stability).
Parameters:
scale: A learnable scaling parameter (initialized to ones) that allows the model to adjust the normalized output’s scale.shift: A learnable shifting parameter (initialized to zeros) that allows the model to adjust the normalized output’s mean.
Forward Pass:
- Calculates the mean and variance of the input tensor
xalong the last dimension for each sample. - Normalizes the input: $\text{normalized}_x = \frac{x – \text{mean}}{\sqrt{\text{variance} + \epsilon}}$
- Applies the learnable scale (
scale) and shift (shift) to the normalized tensor. - Returns the final output.
- Calculates the mean and variance of the input tensor
Key Points¶
- Layer normalization is performed per sample, across the feature dimension, making it suitable for variable-length sequences and transformer models.
- The use of
epsensures numerical stability by preventing division by zero. - Learnable parameters (
scaleandshift) allow the model to recover the original distribution if needed. - This implementation closely mirrors PyTorch’s built-in
nn.LayerNorm, but is written from scratch for educational clarity and flexibility.
Usage¶
This custom LayerNorm class can be used in place of PyTorch’s built-in layer normalization in neural network modules, especially when you want to understand, customize, or experiment with normalization behavior.
class LayerNorm(nn.Module):
def __init__(self, embedding_dim, eps = 1e-5):
super().__init__()
self.eps = eps
self.scale = nn.Parameter(torch.ones(embedding_dim))
self.shift = nn.Parameter(torch.zeros(embedding_dim))
def forward(self, x):
mean = x.mean(dim = -1, keepdim = True)
variance = x.var(dim = -1, keepdim = True, unbiased = False)
normalized_x = (x - mean) / torch.sqrt(variance + self.eps)
return self.scale * normalized_x + self.shift
Using the Custom LayerNorm Class¶
This code cell demonstrates how to use the custom LayerNorm class defined above to normalize a batch of data in PyTorch.
Steps Explained¶
LayerNorm Instantiation
- Creates an instance of the custom
LayerNormclass withembedding_dim = 6, matching the feature dimension of the input batch (ex_batch).
- Creates an instance of the custom
Applying Layer Normalization
- Passes the batch tensor
ex_batchthrough theLayerNorminstance to obtainnormalized_output. - Prints the normalized output tensor.
- Passes the batch tensor
Verifying Normalization
- Calculates and prints the mean and variance of the normalized output along the last dimension for each sample in the batch.
- The mean should be close to zero and the variance close to one, confirming that the normalization is working as intended (modulo learnable parameters, which are initialized to scale=1 and shift=0).
Notes¶
- This example shows how to use a custom normalization layer in practice, similar to how you would use PyTorch’s built-in
nn.LayerNorm. - Layer normalization is applied independently to each sample (row) in the batch, across the feature dimension.
- The learnable parameters (
scaleandshift) allow the model to adapt the normalized output during training. - This approach is essential in transformer models and other deep learning architectures to ensure stable and efficient training.
layer_norm = LayerNorm(embedding_dim = 6)
normalized_output = layer_norm(ex_batch)
print(f"Layer Norm Output: \n {normalized_output}")
mean_after_norm = normalized_output.mean(dim = -1, keepdim = True)
variance_after_norm = normalized_output.var(dim = -1, keepdim = True, unbiased = False)
print(f"Mean After Layer Norm: \n {mean_after_norm}")
print(f"Variance After Layer Norm: \n {variance_after_norm}")
Layer Norm Output:
tensor([[-1.3450, 1.1168, -0.1748, -0.5987, -0.5124, 1.5140],
[-1.2331, 0.8340, 0.8506, 1.1080, -0.2246, -1.3349]],
grad_fn=<AddBackward0>)
Mean After Layer Norm:
tensor([[-3.9736e-08],
[-1.9868e-08]], grad_fn=<MeanBackward1>)
Variance After Layer Norm:
tensor([[1.0000],
[1.0000]], grad_fn=<VarBackward0>)
Custom GELU Activation Function in PyTorch¶
This markdown explains the implementation and purpose of the custom GELU (Gaussian Error Linear Unit) activation function defined in the following code cell.
What is GELU?¶
- GELU is an activation function commonly used in transformer-based models, such as BERT and GPT.
- It is defined as: $$ \text{GELU}(x) = 0.5x \left[1 + \tanh\left(\sqrt{\frac{2}{\pi}}\left(x + 0.044715x^3\right)\right)\right] $$
- GELU provides a smooth, non-linear transformation, allowing the network to learn complex patterns more effectively than traditional activations like ReLU.
Code Explanation¶
- Class Definition:
GELUinherits fromnn.Module, making it compatible with PyTorch models and layers.
- Constructor (
__init__):- Calls the superclass constructor. No additional parameters are needed for GELU.
- Forward Method:
- Implements the GELU formula using PyTorch operations.
- The expression uses
torch.tanhandtorch.powto compute the non-linear transformation. - The constant $0.044715$ is an approximation used in the original paper for computational efficiency.
Why Use GELU?¶
- GELU is preferred in modern transformer architectures because:
- It provides smoother gradients than ReLU, improving optimization.
- It enables better performance in deep networks, especially for NLP tasks.
- It is the default activation in models like BERT and GPT-2/3.
Usage Example¶
To use this custom GELU activation in a PyTorch model:
gelu = GELU()
output = gelu(input_tensor)
This can be used as a drop-in replacement for nn.GELU or F.gelu in custom model architectures.
References¶
class GELU(nn.Module):
def __init__(self):
super().__init__()
def forward(self, x):
return 0.5 * x *(1 + torch.tanh(torch.sqrt(torch.tensor(2.0 / torch.pi)) * (x + 0.044715 * torch.pow(x, 3))))
FeedForward Network in Transformer Models¶
This markdown explains the implementation and role of the FeedForward class defined in the following code cell, which is a core component of transformer-based architectures like GPT and BERT.
What is a FeedForward Network?¶
- In transformer models, each transformer block contains a position-wise feedforward network (FFN) that processes each token’s embedding independently after the self-attention mechanism.
- The FFN typically consists of two linear (fully connected) layers with a non-linear activation function in between.
Code Explanation¶
Class Definition:
FeedForwardinherits fromnn.Module, making it compatible with PyTorch models.- The constructor takes a
configdictionary containing model hyperparameters.
Layers:
- The FFN is implemented as a
nn.Sequentialcontainer with three layers:nn.Linear(config["embedding_dim"], 4 * config["embedding_dim"]): Expands the embedding dimension by a factor of 4 (a common practice in transformer models).GELU(): Applies the custom Gaussian Error Linear Unit activation function for non-linearity.nn.Linear(4 * config["embedding_dim"], config["embedding_dim"]): Projects the expanded dimension back to the original embedding size.
- The FFN is implemented as a
Forward Method:
- The
forwardmethod passes the input tensorxthrough the sequential layers, returning the transformed output.
- The
Why Use This Structure?¶
- The two-layer FFN allows the model to learn complex transformations for each token independently, increasing the model’s capacity and expressiveness.
- The use of the GELU activation provides smooth, non-linear behavior, which is beneficial for deep learning optimization.
- Expanding and then reducing the embedding dimension enables the network to capture richer representations before projecting back to the original size.
Usage in Transformers¶
- In a transformer block, the FFN is applied after the self-attention mechanism and before the residual connection and layer normalization.
- This structure is standard in models like GPT-2, GPT-3, and BERT.
class FeedForward(nn.Module):
def __init__(self, config):
super().__init__()
self.layers = nn.Sequential(
nn.Linear(config["embedding_dim"], 4 * config["embedding_dim"]),
GELU(),
nn.Linear(4 * config["embedding_dim"], config["embedding_dim"])
)
def forward(self, x):
return self.layers(x)
Example: Using the FeedForward Network¶
This markdown explains the demonstration code for instantiating and running the FeedForward network defined earlier in the notebook.
What Does This Code Do?¶
- Instantiates the
FeedForwardclass using the model configuration dictionary (SYDSGPT_CONFIG_345M). - Creates an example input tensor of shape
(2, 6, embedding_dim), representing a batch of 2 sequences, each with 6 tokens, and each token represented by a vector of sizeembedding_dim. - Runs the input through the feedforward network to obtain the output tensor.
- Prints the shape and values of the output tensor for inspection.
Step-by-Step Explanation¶
FeedForward Instantiation
feed_forward = FeedForward(SYDSGPT_CONFIG_345M)- Creates a feedforward network with the same embedding dimension as the model configuration.
Example Input Creation
example_input = torch.randn(2, 6, SYDSGPT_CONFIG_345M["embedding_dim"])- Generates a random tensor to simulate a batch of token embeddings.
- Shape:
(batch_size, sequence_length, embedding_dim).
Forward Pass
output = feed_forward(example_input)- Passes the input through the feedforward network, applying two linear transformations and a GELU activation in between.
Output Inspection
- Prints the shape and values of the output tensor.
- The output shape matches the input:
(2, 6, embedding_dim), since the feedforward network projects back to the original embedding size.
Why Is This Important?¶
- This example shows how to use the feedforward network as part of a transformer block, processing each token’s embedding independently.
- The feedforward network is a key component in transformer architectures, enabling the model to learn complex, non-linear transformations for each token.
- Understanding the input and output shapes is crucial for integrating the feedforward network into larger models.
Usage in Practice¶
- In a full transformer model, this feedforward network would be used after the self-attention mechanism and before layer normalization and residual connections.
- The pattern of expanding and reducing the embedding dimension is standard in transformer-based models like GPT and BERT.
feed_forward = FeedForward(SYDSGPT_CONFIG_345M)
example_input = torch.randn(2, 6, SYDSGPT_CONFIG_345M["embedding_dim"])
output = feed_forward(example_input)
print(f"Feed Forward Output Shape: {output.shape}")
print(f"Feed Forward Output: \n {output}")
Feed Forward Output Shape: torch.Size([2, 6, 1024])
Feed Forward Output:
tensor([[[ 0.0212, -0.2190, 0.2352, ..., 0.1612, 0.3023, -0.1417],
[-0.2370, 0.0163, 0.2842, ..., 0.1003, 0.0263, -0.0122],
[-0.1790, 0.0294, -0.0350, ..., 0.0320, 0.2061, -0.1103],
[ 0.1206, 0.0419, 0.0231, ..., -0.0099, -0.1882, -0.2501],
[ 0.0942, -0.2093, 0.3045, ..., -0.2473, 0.1754, -0.1967],
[ 0.0837, 0.1889, 0.1583, ..., 0.2284, 0.2347, -0.1868]],
[[-0.4378, -0.0083, 0.1454, ..., 0.0780, -0.0978, 0.0250],
[ 0.0409, -0.1573, 0.2250, ..., 0.2111, -0.2130, 0.1422],
[ 0.3191, -0.2163, 0.0870, ..., -0.2538, -0.0757, -0.1970],
[ 0.0511, 0.0946, 0.2757, ..., 0.0645, 0.1366, -0.1490],
[ 0.2247, -0.1286, 0.1931, ..., -0.1176, 0.4198, 0.1183],
[ 0.3904, -0.3158, 0.2139, ..., 0.2581, 0.1807, -0.2763]]],
grad_fn=<ViewBackward0>)
Residual Connections and Gradient Flow: Demonstration¶
This markdown explains the code cell that demonstrates the effect of residual (shortcut) connections on gradient flow in deep neural networks, a key concept in modern architectures like transformers and ResNets.
What Does This Code Do?¶
- Defines a test neural network class (
ResidualConnectionsTestNN) with multiple layers, optionally using residual (shortcut) connections. - Implements a function (
get_gradients) to compute and print the mean absolute value of gradients for each layer’s weights after a backward pass. - Compares two models: one with residual connections and one without, using the same architecture and input.
- Prints the mean of gradients for each layer in both cases, illustrating the impact of residual connections on gradient propagation.
Step-by-Step Explanation¶
ResidualConnectionsTestNN Class
- Takes a list of layer dimensions and a boolean
use_shortcutsto control whether residual connections are used. - Builds a sequence of layers, each consisting of a linear transformation followed by a GELU activation.
- In the
forwardmethod, ifuse_shortcutsisTrueand the input and output shapes match, adds the input to the output (residual connection). Otherwise, just uses the output.
- Takes a list of layer dimensions and a boolean
get_gradients Function
- Runs a forward pass, computes a simple MSE loss against a target, and performs backpropagation.
- Prints the mean absolute value of the gradients for each weight parameter in the model.
Experiment Setup
- Defines a simple input tensor and a list of layer dimensions for a 6-layer network.
- Instantiates two models with the same random seed: one with residual connections, one without.
- Runs the gradient computation for both models and prints the results.
Why Are Residual Connections Important?¶
- Gradient Flow: Residual connections help gradients flow backward through deep networks, reducing the risk of vanishing gradients and enabling the training of much deeper models.
- Stability: They make optimization easier and more stable, especially in very deep architectures.
- Standard Practice: Residual connections are a standard component in transformer models (e.g., GPT, BERT) and ResNets.
What Should You Observe?¶
- The mean of gradients in the model with residual connections should generally be larger and more evenly distributed across layers, indicating better gradient flow.
- In the model without residuals, gradients may diminish rapidly in deeper layers, illustrating the vanishing gradient problem.
class ResidualConnectionsTestNN(nn.Module):
def __init__(self, layer_dims, use_shortcuts):
super().__init__()
self.use_shortcuts = use_shortcuts
self.layers = nn.ModuleList([
nn.Sequential(nn.Linear(layer_dims[0], layer_dims[1]), GELU()),
nn.Sequential(nn.Linear(layer_dims[1], layer_dims[2]), GELU()),
nn.Sequential(nn.Linear(layer_dims[2], layer_dims[3]), GELU()),
nn.Sequential(nn.Linear(layer_dims[3], layer_dims[4]), GELU()),
nn.Sequential(nn.Linear(layer_dims[4], layer_dims[5]), GELU()),
nn.Sequential(nn.Linear(layer_dims[5], layer_dims[6]), GELU())
])
def forward(self, x):
for layer in self.layers:
layer_output = layer(x)
if self.use_shortcuts and x.shape == layer_output.shape:
x = x + layer_output
else:
x = layer_output
return x
def get_gradients(model, input):
output = model(input)
target = torch.tensor([[0.]])
loss_function = nn.MSELoss()
loss = loss_function(output, target)
loss.backward()
for name, param in model.named_parameters():
if 'weight' in name:
print(f"Mean of Gradients for {name}: {param.grad.abs().mean().item()}")
layer_dims = [3, 3, 3, 3, 3, 3, 1]
input = torch.tensor([[-1., 0., 1.]])
torch.manual_seed(246)
model_without_residuals = ResidualConnectionsTestNN(layer_dims, use_shortcuts = False)
torch.manual_seed(246)
model_with_residuals = ResidualConnectionsTestNN(layer_dims, use_shortcuts = True)
print("Gradients without Residual Connections:")
get_gradients(model_without_residuals, input)
print("Gradients with Residual Connections:")
get_gradients(model_with_residuals, input)
Gradients without Residual Connections: Mean of Gradients for layers.0.0.weight: 2.173086795664858e-05 Mean of Gradients for layers.1.0.weight: 1.2031879123242106e-05 Mean of Gradients for layers.2.0.weight: 4.762777825817466e-05 Mean of Gradients for layers.3.0.weight: 0.0004226445162203163 Mean of Gradients for layers.4.0.weight: 0.0009699637885205448 Mean of Gradients for layers.5.0.weight: 0.0055029913783073425 Gradients with Residual Connections: Mean of Gradients for layers.0.0.weight: 0.0026402678340673447 Mean of Gradients for layers.1.0.weight: 0.0009344664285890758 Mean of Gradients for layers.2.0.weight: 0.004430014174431562 Mean of Gradients for layers.3.0.weight: 0.00808763224631548 Mean of Gradients for layers.4.0.weight: 0.004049395211040974 Mean of Gradients for layers.5.0.weight: 0.06586597859859467
Transformer Block: Architecture and Residual Connections¶
This markdown explains the implementation and design of the TransformerBlock class, a core building block in transformer-based models such as GPT and BERT.
Overview¶
- The transformer block combines multi-head self-attention, feedforward networks, layer normalization, dropout, and residual (shortcut) connections.
- This structure enables the model to learn complex dependencies and representations efficiently, while maintaining stable training in deep architectures.
Components Explained¶
Multi-Head Attention (
self.attention)- Uses the imported
MultiHeadAttentionmodule to perform self-attention across the input sequence. - Allows the model to focus on different parts of the sequence simultaneously, capturing various relationships between tokens.
- Configured with input/output dimensions, dropout, context length, number of heads, and optional bias.
- Uses the imported
Layer Normalization (
self.layer_norm1,self.layer_norm2)- Normalizes the input to each sub-layer, stabilizing and accelerating training.
- Applied before both the attention and feedforward sub-layers (pre-norm architecture).
FeedForward Network (
self.feed_forward)- Applies a position-wise feedforward network to each token embedding independently.
- Consists of two linear layers with a GELU activation in between (see earlier notebook cells for details).
Dropout (
self.dropout)- Randomly zeroes some elements of the input tensor during training, helping prevent overfitting.
- Applied after both the attention and feedforward sub-layers.
Residual Connections
- Adds the input of each sub-layer to its output (“shortcut”), enabling better gradient flow and more stable optimization.
- Two residual connections: one after attention, one after feedforward.
Forward Pass Logic¶
First Residual Block (Attention):
- Save the input as
shortcut. - Apply layer normalization, then multi-head attention, then dropout.
- Add the original input (
shortcut) to the output (residual connection).
- Save the input as
Second Residual Block (FeedForward):
- Save the new input as
shortcut. - Apply layer normalization, then the feedforward network, then dropout.
- Add the input (
shortcut) to the output (residual connection).
- Save the new input as
Return the final output.
Why This Structure?¶
- Residual connections help gradients flow through deep networks, making it possible to train very deep transformer models.
- Layer normalization before each sub-layer (pre-norm) improves stability and convergence, especially in large models.
- Multi-head attention and feedforward networks are the two main sub-layers in each transformer block, enabling the model to learn both contextual and token-specific representations.
Usage in Transformers¶
- This block is stacked multiple times in transformer architectures (e.g., 12, 24, or more layers).
- The output of one block is the input to the next, allowing the model to build increasingly complex representations.
from attention.MultiHeadAttention import MultiHeadAttention
class TransformerBlock(nn.Module):
def __init__(self, config):
super().__init__()
self.attention = MultiHeadAttention(
input_dim = config["embedding_dim"],
output_dim = config["embedding_dim"],
dropout = config["dropout"],
context_length = config["context_length"],
num_heads = config["num_heads"],
qkv_bias = config["qkv_bias"])
self.layer_norm1 = LayerNorm(config["embedding_dim"])
self.feed_forward = FeedForward(config)
self.layer_norm2 = LayerNorm(config["embedding_dim"])
self.dropout = nn.Dropout(config["dropout"])
def forward(self, x):
shortcut = x
x = self.layer_norm1(x)
x = self.attention(x)
x = self.dropout(x)
x = x + shortcut
shortcut = x
x = self.layer_norm2(x)
x = self.feed_forward(x)
x = self.dropout(x)
x = x + shortcut
return x
Example: Running a Transformer Block on Input Data¶
This markdown explains the demonstration code for instantiating and running the TransformerBlock on a batch of example input data.
What Does This Code Do?¶
- Sets a manual random seed for reproducibility using
torch.manual_seed(246). - Instantiates the
TransformerBlockclass with the model configuration dictionary (SYDSGPT_CONFIG_345M). - Creates an example input tensor of shape
(2, 6, embedding_dim), representing a batch of 2 sequences, each with 6 tokens, and each token represented by a vector of sizeembedding_dim. - Runs the input through the transformer block to obtain the output tensor.
- Prints the shape and values of both the input and output tensors for inspection.
Step-by-Step Explanation¶
Random Seed Setup
torch.manual_seed(246)ensures that the random numbers generated (for the input tensor and model initialization) are reproducible.
Transformer Block Instantiation
transformer = TransformerBlock(SYDSGPT_CONFIG_345M)creates a transformer block using the specified configuration.
Example Input Creation
example_input = torch.randn(2, 6, SYDSGPT_CONFIG_345M["embedding_dim"])generates a random tensor to simulate a batch of token embeddings.- Shape:
(batch_size, sequence_length, embedding_dim).
Forward Pass
output = transformer(example_input)passes the input through the transformer block, applying multi-head attention, feedforward network, layer normalization, dropout, and residual connections.
Output Inspection
- Prints the shape and values of the input and output tensors.
- The output shape matches the input:
(2, 6, embedding_dim), since the transformer block preserves the sequence and embedding dimensions.
Why Is This Important?¶
- This example shows how to use a transformer block as part of a larger model, processing batches of token embeddings.
- The transformer block is a key component in architectures like GPT and BERT, enabling the model to learn complex relationships and representations.
- Understanding the input and output shapes is crucial for integrating transformer blocks into deep learning pipelines.
Usage in Practice¶
- In a full transformer model, multiple transformer blocks are stacked to process input sequences, with each block building on the representations learned by the previous one.
- The pattern of using random input data is common for testing and debugging model components.
torch.manual_seed(246)
transformer = TransformerBlock(SYDSGPT_CONFIG_345M)
example_input = torch.randn(2, 6, SYDSGPT_CONFIG_345M["embedding_dim"])
output = transformer(example_input)
print(f"Example Input Shape: {example_input.shape}")
print(f"Transformer Block Output Shape: {output.shape}")
print(f"Transformer Block Output: \n {output}")
Example Input Shape: torch.Size([2, 6, 1024])
Transformer Block Output Shape: torch.Size([2, 6, 1024])
Transformer Block Output:
tensor([[[ 2.6021, -0.6464, -1.1488, ..., -0.1816, -1.0399, -0.2072],
[-0.4377, 1.4974, -1.1613, ..., 0.2095, -0.7198, -2.3146],
[ 1.7130, 0.8384, 0.0355, ..., 0.4016, -0.5036, -1.5147],
[ 0.4436, -0.5751, -1.2977, ..., -2.1431, -1.8006, 1.2133],
[ 0.9577, 1.0001, -2.2591, ..., -1.0065, 0.3973, 0.6356],
[-0.2310, -0.9183, 0.0729, ..., 0.7959, -0.8819, 0.5912]],
[[-1.4568, -1.9117, -0.2138, ..., 0.5810, -1.6277, -2.8289],
[ 0.3885, 1.0216, -0.5874, ..., -0.3243, 1.3307, -0.8727],
[-1.2116, -0.2976, -0.3767, ..., 1.7585, 0.1871, -0.5062],
[ 0.0051, -1.5070, -1.0969, ..., -0.2433, -0.8636, 0.0646],
[ 0.0226, 0.1599, 1.1637, ..., -1.2578, 1.5422, -2.0616],
[ 1.1118, 1.3035, -0.0383, ..., -1.6219, -1.5757, -2.3353]]],
grad_fn=<AddBackward0>)
Transformer Block Output Shape: torch.Size([2, 6, 1024])
Transformer Block Output:
tensor([[[ 2.6021, -0.6464, -1.1488, ..., -0.1816, -1.0399, -0.2072],
[-0.4377, 1.4974, -1.1613, ..., 0.2095, -0.7198, -2.3146],
[ 1.7130, 0.8384, 0.0355, ..., 0.4016, -0.5036, -1.5147],
[ 0.4436, -0.5751, -1.2977, ..., -2.1431, -1.8006, 1.2133],
[ 0.9577, 1.0001, -2.2591, ..., -1.0065, 0.3973, 0.6356],
[-0.2310, -0.9183, 0.0729, ..., 0.7959, -0.8819, 0.5912]],
[[-1.4568, -1.9117, -0.2138, ..., 0.5810, -1.6277, -2.8289],
[ 0.3885, 1.0216, -0.5874, ..., -0.3243, 1.3307, -0.8727],
[-1.2116, -0.2976, -0.3767, ..., 1.7585, 0.1871, -0.5062],
[ 0.0051, -1.5070, -1.0969, ..., -0.2433, -0.8636, 0.0646],
[ 0.0226, 0.1599, 1.1637, ..., -1.2578, 1.5422, -2.0616],
[ 1.1118, 1.3035, -0.0383, ..., -1.6219, -1.5757, -2.3353]]],
grad_fn=<AddBackward0>)
SydsGPT Model: Full GPT-2 Style Architecture¶
This markdown explains the implementation and design of the SydsGPT class, which represents a complete GPT-2 style transformer language model built using PyTorch. This class brings together all the core components defined earlier in the notebook, including embeddings, transformer blocks, normalization, and output projection.
Overview of the SydsGPT Class¶
- Purpose: Implements a full transformer-based language model, similar to GPT-2, capable of processing sequences of tokenized text and generating predictions for the next token in a sequence.
- Structure: The model is composed of several key submodules, each responsible for a specific part of the computation pipeline.
Components Explained¶
Token Embedding (
self.token_embedding)- Maps each input token (integer ID) to a high-dimensional vector representation of size
embedding_dim. - Allows the model to learn semantic relationships between tokens.
- Maps each input token (integer ID) to a high-dimensional vector representation of size
Position Embedding (
self.position_embedding)- Adds information about the position of each token in the sequence, enabling the model to distinguish between tokens at different positions.
- Essential for transformer models, which lack inherent sequence order awareness.
Dropout on Embeddings (
self.drop_embedding)- Applies dropout to the sum of token and position embeddings, helping prevent overfitting during training.
Stacked Transformer Blocks (
self.transformer_blocks)- A sequence of
num_layerstransformer blocks, each containing multi-head self-attention, feedforward networks, layer normalization, dropout, and residual connections. - Each block refines the token representations by attending to other tokens and applying non-linear transformations.
- A sequence of
Final Layer Normalization (
self.final_layer_norm)- Normalizes the output of the last transformer block, stabilizing training and improving convergence.
Output Projection (
self.output_projection)- Projects the final hidden states to the vocabulary size, producing logits for each token position.
- These logits are used to predict the next token in the sequence during training or inference.
Forward Pass Logic¶
- Input:
- Expects an input tensor of shape
(batch_size, sequence_length), where each element is a token ID.
- Expects an input tensor of shape
- Embedding:
- Computes token and position embeddings, sums them, and applies dropout.
- Transformer Blocks:
- Passes the embeddings through the stack of transformer blocks, allowing the model to learn complex dependencies and contextual representations.
- Normalization and Output:
- Applies final layer normalization and projects the result to the vocabulary size, producing logits for each token position.
- Return:
- Returns the logits tensor of shape
(batch_size, sequence_length, vocab_size).
- Returns the logits tensor of shape
Why This Structure?¶
- Scalability: The modular design allows for easy scaling by adjusting the number of layers, embedding size, and other hyperparameters.
- Expressiveness: Stacking multiple transformer blocks enables the model to capture deep, hierarchical relationships in text.
- Standard Practice: This architecture closely follows the design of GPT-2 and similar large language models, making it suitable for a wide range of NLP tasks.
Usage in Practice¶
- The
SydsGPTclass can be instantiated with a configuration dictionary and used for training or inference on tokenized text data. - During training, the model’s output logits are typically passed to a loss function (e.g., cross-entropy) to optimize the model parameters.
- For text generation, the model can be used in an autoregressive fashion, predicting one token at a time based on previous context.
Summary Table of Key Components¶
| Component | Purpose | Output Shape |
|---|---|---|
| Token Embedding | Learnable token representations | (batch_size, seq_length, emb_dim) |
| Position Embedding | Learnable position information | (batch_size, seq_length, emb_dim) |
| Dropout | Regularization on embeddings | (batch_size, seq_length, emb_dim) |
| Transformer Blocks | Contextualize token representations | (batch_size, seq_length, emb_dim) |
| Final Layer Norm | Normalize final hidden states | (batch_size, seq_length, emb_dim) |
| Output Projection | Project to vocabulary logits | (batch_size, seq_length, vocab_size) |
This class serves as the backbone of a GPT-2 style language model, integrating all the essential components for modern transformer-based NLP.
class SydsGPT(nn.Module):
def __init__(self, config):
super().__init__()
self.token_embedding = nn.Embedding(config["vocab_size"], config["embedding_dim"])
self.position_embedding = nn.Embedding(config["context_length"], config["embedding_dim"])
self.drop_embedding = nn.Dropout(config["dropout"])
self.transformer_blocks = nn.Sequential(*[TransformerBlock(config) for _ in range(config["num_layers"])])
self.final_layer_norm = LayerNorm(config["embedding_dim"])
self.output_projection = nn.Linear(config["embedding_dim"], config["vocab_size"], bias = False)
def forward(self, input):
batch_size, seq_length = input.shape
token_embeddings = self.token_embedding(input)
position_embeddings = self.position_embedding(torch.arange(seq_length, device=input.device))
x = token_embeddings + position_embeddings
x = self.drop_embedding(x)
x = self.transformer_blocks(x)
x = self.final_layer_norm(x)
logits = self.output_projection(x)
return logits
Example: Running the Full SydsGPT Model on Tokenized Input¶
This markdown explains the demonstration code for instantiating and running the full SydsGPT model on a batch of tokenized input data. This example shows how to use the complete transformer-based language model defined in the previous cell.
What Does This Code Do?¶
- Sets a manual random seed for reproducibility using
torch.manual_seed(246). - Instantiates the
SydsGPTclass with the model configuration dictionary (SYDSGPT_CONFIG_345M). - Runs a batch of tokenized input data (created earlier in the notebook) through the model to obtain output logits.
- Prints the input batch, the shape of the logits tensor, and the logits themselves for inspection.
Step-by-Step Explanation¶
Random Seed Setup
torch.manual_seed(246)ensures that the random numbers generated for model initialization are reproducible.
Model Instantiation
sydsgpt_model = SydsGPT(SYDSGPT_CONFIG_345M)creates an instance of the full transformer model using the specified configuration.
Forward Pass
logits = sydsgpt_model(batch)passes the tokenized input batch through the model.- The model processes the input through embeddings, stacked transformer blocks, normalization, and output projection to produce logits for each token position.
Output Inspection
- Prints the input batch tensor for reference.
- Prints the shape of the logits tensor, which should be
(batch_size, sequence_length, vocab_size). - Prints the logits tensor itself, which contains the unnormalized predictions for each token position in the input.
Why Is This Important?¶
- This example demonstrates how to use the full transformer model for inference or training on tokenized text data.
- The output logits can be used to compute loss during training (e.g., with cross-entropy) or to generate text by sampling or selecting the most likely next token.
- Understanding the input and output shapes is crucial for integrating the model into larger NLP pipelines.
Usage in Practice¶
- In a real-world scenario, the input batch would be created by tokenizing raw text using a tokenizer (as shown earlier in the notebook).
- The model can be trained on large text corpora to learn language patterns, or used for downstream tasks such as text generation, completion, or classification.
- The logits output by the model are typically passed to a softmax function to obtain probabilities over the vocabulary for each token position.
This cell provides a practical example of running a complete GPT-2 style model on tokenized input, serving as a template for further experimentation and development.
torch.manual_seed(246)
sydsgpt_model = SydsGPT(SYDSGPT_CONFIG_345M)
logits = sydsgpt_model(batch)
print(f"Input: {batch}")
print(f"Logits Shape: {logits.shape}")
print(f"Logits: {logits}")
Input: tensor([[15496, 703, 389, 345],
[ 2061, 389, 345, 1804]])
Logits Shape: torch.Size([2, 4, 50257])
Logits: tensor([[[ 0.1230, 0.3697, -0.4113, ..., -0.0493, -0.4047, -0.3231],
[ 0.3657, -0.0389, -0.2145, ..., -0.2732, -0.2118, -0.7021],
[ 0.5050, -0.6050, 0.2186, ..., -0.7836, -0.2520, -0.2040],
[ 0.3738, 0.2956, 0.5254, ..., 1.0762, -0.7500, -0.0704]],
[[ 0.5839, -0.2989, -0.1086, ..., -0.3229, -0.1380, -0.2090],
[-0.0806, 0.2465, -0.0125, ..., -1.4313, -0.6350, -0.6414],
[-0.5175, -0.8065, 0.2659, ..., 0.6558, -0.1612, -0.0930],
[ 0.5556, -0.1440, 0.0022, ..., 1.2245, -0.1364, -0.6378]]],
grad_fn=<UnsafeViewBackward0>)
Calculating Total Parameters in the SydsGPT Model¶
This markdown explains the code cell that calculates and prints the total number of trainable parameters in the SydsGPT model. Understanding the parameter count is crucial for assessing the model’s size, memory requirements, and computational complexity.
What Does This Code Do?¶
- Computes the total number of parameters in the
SydsGPTmodel by summing the number of elements in each parameter tensor. - Prints the total parameter count, providing insight into the model’s scale (e.g., whether it matches the intended “345M” parameter target).
Step-by-Step Explanation¶
Parameter Counting
sydsgpt_model.parameters()returns an iterator over all trainable parameters (weights and biases) in the model.- For each parameter tensor,
parameter.numel()returns the total number of elements (i.e., the number of scalars in that tensor). - The
sum(...)function adds up the element counts for all parameters, yielding the total number of trainable parameters in the model.
Printing the Result
- The total parameter count is printed in a human-readable format.
Why Is This Important?¶
- Model Size: The number of parameters directly determines the model’s memory footprint and computational requirements.
- Benchmarking: Comparing parameter counts helps benchmark against other models (e.g., GPT-2 small, medium, large, XL).
- Resource Planning: Knowing the parameter count is essential for planning training hardware (GPUs/TPUs), estimating training time, and managing deployment constraints.
- Sanity Check: Ensures that the model architecture matches the intended design (e.g., “345M” parameters for a GPT-2 medium-sized model).
Usage in Practice¶
- This code can be used after defining or modifying a model to quickly check its size.
- For large models, parameter counts are often reported in millions (M) or billions (B). For example, a value of
345,000,000means the model has 345 million parameters. - The parameter count should be consistent with the model’s configuration (number of layers, embedding size, etc.).
This cell provides a simple but essential check for anyone developing or experimenting with deep learning models, especially large-scale transformer architectures.
total_parameters = sum(parameter.numel() for parameter in sydsgpt_model.parameters())
print(f"Total Parameters in SydsGPT Model: {total_parameters}")
Total Parameters in SydsGPT Model: 406212608
Estimating the SydsGPT Model’s Memory Footprint¶
This markdown explains the code cell that estimates and prints the total memory size of the SydsGPT model in megabytes (MB). Understanding the memory requirements is essential for planning training, deployment, and hardware selection for large neural networks.
What Does This Code Do?¶
- Calculates the total memory size of all model parameters, assuming each parameter is stored as a 32-bit (4-byte) floating-point number (the default in PyTorch).
- Prints the total model size in megabytes (MB), providing a practical sense of the model’s memory footprint.
Step-by-Step Explanation¶
Parameter Size Calculation
total_parametersis the total number of trainable parameters in the model (computed in the previous cell).- Each parameter is assumed to be a 32-bit float, which occupies 4 bytes of memory.
total_size_bytes = total_parameters * 4computes the total size in bytes.
Conversion to Megabytes
total_size_mb = total_size_bytes / (1024 ** 2)converts the size from bytes to megabytes (1 MB = 1,048,576 bytes).- This makes the result more interpretable and easier to compare with available system or GPU memory.
Printing the Result
- The total model size is printed with two decimal places for clarity.
Why Is This Important?¶
- Hardware Planning: Knowing the model’s memory footprint is crucial for selecting appropriate hardware (e.g., GPU/TPU with sufficient VRAM).
- Training Feasibility: Large models may not fit into memory on smaller devices, requiring model parallelism, gradient checkpointing, or other memory-saving techniques.
- Deployment: Understanding memory requirements helps when deploying models to production environments, especially for edge or mobile devices.
- Optimization: Memory usage can be a bottleneck; knowing the size helps guide optimization efforts (e.g., quantization, pruning, mixed precision).
Usage in Practice¶
- This calculation assumes all parameters are stored as 32-bit floats. If using mixed precision (e.g., float16), the memory footprint would be roughly halved.
- The reported size does not include additional memory used for activations, gradients, optimizer states, or temporary buffers during training or inference.
- For very large models, memory requirements can quickly exceed the capacity of a single device, necessitating distributed or sharded training.
This cell provides a quick and practical estimate of the model’s memory requirements, which is essential for anyone working with large-scale deep learning models.
total_size_bytes = total_parameters * 4
total_size_mb = total_size_bytes / (1024 ** 2)
print(f"Total Model Size: {total_size_mb:.2f} MB")
Total Model Size: 1549.58 MB
Simple Greedy Text Generation Function for SydsGPT¶
This markdown explains the code cell that defines generate_simple, a basic text generation function for the SydsGPT model. This function demonstrates how to use a trained language model to generate sequences of tokens in an autoregressive (one token at a time) fashion.
What Does This Code Do?¶
- Implements a simple greedy decoding loop for generating text from a transformer-based language model.
- Takes an initial sequence of token IDs and repeatedly predicts and appends the most likely next token, up to a specified maximum length.
- Handles context windowing to ensure the model only sees the most recent tokens up to its maximum context size.
Step-by-Step Explanation¶
Function Signature
generate_simple(model, input_ids, max_length, context_size)model: The language model (e.g.,SydsGPT) to use for generation.input_ids: A tensor of shape(batch_size, current_sequence_length)containing the initial token IDs for each sequence in the batch.max_length: The number of new tokens to generate.context_size: The maximum number of tokens the model can attend to (should match the model’s context window, e.g., 1024).
Generation Loop
- For each step up to
max_length:- Context Cropping:
input_ids_crop = input_ids[:, -context_size:]ensures that only the most recentcontext_sizetokens are fed to the model, respecting the model’s context window.
- Model Forward Pass:
logits = model(input_ids_crop)computes the output logits for the current context.torch.no_grad()disables gradient computation for efficiency.
- Next Token Selection:
next_token_logits = logits[:, -1, :]extracts the logits for the last position in the sequence (the next token to predict).next_token_probs = torch.softmax(next_token_logits, dim = -1)converts logits to probabilities over the vocabulary.next_token = torch.argmax(next_token_probs, dim = -1, keepdim = True)selects the most likely next token (greedy decoding).
- Sequence Extension:
input_ids = torch.cat((input_ids, next_token), dim = 1)appends the predicted token to the sequence for the next iteration.
- Context Cropping:
- For each step up to
Return Value
- Returns the final tensor of token IDs, now extended by
max_lengthnew tokens for each sequence in the batch.
- Returns the final tensor of token IDs, now extended by
Why Is This Important?¶
- Autoregressive Generation: This function demonstrates the core principle of autoregressive text generation, where each new token is predicted based on all previous tokens.
- Greedy Decoding: The function uses greedy decoding (always picking the most likely token), which is simple but may not produce the most diverse or creative outputs. More advanced methods include sampling, top-k, or nucleus (top-p) sampling.
- Context Management: Properly handling the context window is essential for large models, which may have strict limits on the number of tokens they can process at once.
- Practical Usage: This function can be used to generate text completions, simulate dialogue, or test the model’s ability to extend sequences.
Usage in Practice¶
- To use this function, provide a trained model, an initial sequence of token IDs, the number of tokens to generate, and the model’s context size.
- The output can be decoded back to text using the tokenizer’s
decodemethod. - For more realistic or creative text, consider implementing sampling-based decoding strategies.
This cell provides a clear and practical example of how to perform basic text generation with a transformer-based language model in PyTorch.
def generate_simple(model, input_ids, max_length, context_size):
for _ in range(max_length):
input_ids_crop = input_ids[:, -context_size:]
with torch.no_grad():
logits = model(input_ids_crop)
next_token_logits = logits[:, -1, :]
next_token_probs = torch.softmax(next_token_logits, dim = -1)
next_token = torch.argmax(next_token_probs, dim = -1, keepdim = True)
input_ids = torch.cat((input_ids, next_token), dim = 1)
return input_ids
Text Generation from a Prompt: End-to-End Example¶
This cell shows how to generate text with the SydsGPT model using the generate_simple function and a plain-English prompt.
Prompt and tokenization:
start_context = "Once upon a time"is the starting text.tokenizer.encode(...)converts the prompt into token IDs.torch.tensor(...).unsqueeze(0)adds a batch dimension so the input shape is(batch_size=1, seq_len).
Model eval mode:
sydsgpt_model.eval()disables dropout and gradients for deterministic, faster inference.
Generation loop (greedy decoding):
context_size = SYDSGPT_CONFIG_345M["context_length"]sets the max number of tokens the model attends to.generate_simple(model, input_ids, 10, context_size)appends 10 new tokens by repeatedly:- Cropping to the last
context_sizetokens, - Running the model to get logits,
- Taking the argmax token (most probable next token),
- Concatenating it to the sequence.
- Cropping to the last
Decoding:
tokenizer.decode(...)converts the generated token IDs back to readable text.
Notes and tips:
- Greedy decoding is simple and fast, but can be repetitive. For more variety, consider top-k or nucleus (top-p) sampling.
- If your prompt is long, the function automatically crops to the most recent
context_sizetokens to respect the model’s context window. - To generate longer outputs, increase the
max_lengthargument ingenerate_simple.
start_context = "Once upon a time"
encoded_context = tokenizer.encode(start_context)
input_ids = torch.tensor(encoded_context).unsqueeze(0)
print(f"Encoded Context: {encoded_context}")
print(f"Input IDs Shape: {input_ids.shape}")
sydsgpt_model.eval()
context_size = SYDSGPT_CONFIG_345M["context_length"]
generated_ids = generate_simple(sydsgpt_model, input_ids, 10, context_size)
print(f"Generated IDs: {generated_ids}")
generated_text = tokenizer.decode(generated_ids.squeeze(0).tolist())
print(f"Generated Text: {generated_text}")
Encoded Context: [7454, 2402, 257, 640]
Input IDs Shape: torch.Size([1, 4])
Generated IDs: tensor([[ 7454, 2402, 257, 640, 22021, 7857, 44144, 45836, 4328, 41871,
43984, 32880, 11958, 21420]])
Generated Text: Once upon a time theirssize Sharif grunt splrfBangflex penet Nest
Generated IDs: tensor([[ 7454, 2402, 257, 640, 22021, 7857, 44144, 45836, 4328, 41871,
43984, 32880, 11958, 21420]])
Generated Text: Once upon a time theirssize Sharif grunt splrfBangflex penet Nest

Leave a Reply